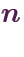”. But even without those axioms, we are confident that “
”. But even without those axioms, we are confident that “



 ” is true. So instead of continuing to prove things like “
” is true. So instead of continuing to prove things like “



 ” or “
” or “



 ” using the same method, I will assume these are provable if needed, and from now on focus on things that we really don’t know if they are true or not.
” using the same method, I will assume these are provable if needed, and from now on focus on things that we really don’t know if they are true or not.1.Integers














 ”. If we include numbers with minus signs (except for
”. If we include numbers with minus signs (except for  ), we get the set of integers. So the set of all integers is “
), we get the set of integers. So the set of all integers is “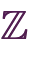





















 ”.
”. are called positive, and numbers less than
are called positive, and numbers less than  are called negative.
are called negative.  is neither positive nor negative.
is neither positive nor negative. and
and  , you can do addition “
, you can do addition “

 ”, subtraction “
”, subtraction “

 ”, and multiplication “
”, and multiplication “

 ”. Multiplication “
”. Multiplication “

 ” is also written as “
” is also written as “

 ”, and often the multiplication sign is omitted and written as “
”, and often the multiplication sign is omitted and written as “
 ”. I will use that style from now on.
”. I will use that style from now on.1.1Exponentiation
 and a non-negative integer
and a non-negative integer  , the number you get by multiplying
, the number you get by multiplying 
 times is called an exponentiation and written as “
times is called an exponentiation and written as “
 ”. For example, “
”. For example, “
 ” means “
” means “



 ”, which is
”, which is  . “
. “

 ” means “
” means “









 ”, which is
”, which is 



 .
. , we define “
, we define “


 ”. For example, “
”. For example, “


 ” and “
” and “





 ”.
”.If you look at “2⁵ = 32”, “2⁴ = 16”, “2³ = 8”, “2² = 4”, “2¹ = 2”, you can see the result is halved each time. So it’s natural to think that “2⁰ = 1”.

 ” is sometimes defined as “
” is sometimes defined as “ ” for convenience, but for various reasons, it is often not defined.
” for convenience, but for various reasons, it is often not defined.One reason why “0⁰” is usually not defined is that if you look at “3⁰ = 1”, “2⁰ = 1”, “1⁰ = 1”, it seems natural to think “0⁰ = 1”. But if you look at “0³ = 0”, “0² = 0”, “0¹ = 0”, it seems natural to think “0⁰ = 0”. These two ideas conflict.

 times” and “
times” and “
 times” gives “
times” gives “


 times”.
times”. s.
s.
 times” repeated
times” repeated  times, so you get “
times, so you get “


 times”.
times”.

 ” repeated
” repeated  times, which becomes “
times, which becomes “
 times and
times and 
 times”.
times”.1.2Absolute Value
 of an integer
of an integer  is called its absolute value, written as “
is called its absolute value, written as “

 ”. For example, “
”. For example, “



 ” and “
” and “




 ”.
”.

 is defined as:
is defined as:
- If


 , then
, then 



 .
. - If


 , then
, then 




 .
.



 , then
, then 

 , so “
, so “












 ”.
”.2.Properties of Integers
2.1Quotient and Remainder


 ), the result is not always an integer. So we define the quotient and remainder to make the result an integer.
), the result is not always an integer. So we define the quotient and remainder to make the result an integer.

 ” is the number of items each person gets when
” is the number of items each person gets when  items are distributed among
items are distributed among  people. The remainder is the number of items left over. For example, “
people. The remainder is the number of items left over. For example, “

 ” gives a quotient of
” gives a quotient of  and a remainder of
and a remainder of  .
.

 has quotient
has quotient  and remainder
and remainder  ” means “distributing
” means “distributing  items among
items among  people gives
people gives  items each and
items each and  left over”. In other words, “
left over”. In other words, “





 ”. So we define the quotient
”. So we define the quotient  and remainder
and remainder 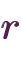 of
of 

 as the numbers that satisfy “
as the numbers that satisfy “



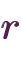

 ”.
”.For integers  and non-zero
and non-zero  , the quotient and remainder of
, the quotient and remainder of 

 are the integers
are the integers  and
and 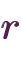 that satisfy:
that satisfy: 



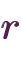

 and
and 

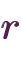

 .
.


 ” gives
” gives 

 and
and 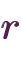

 , and “
, and “





 ” with “
” with “



 ”.
”.

 , the quotient and remainder are not defined. So “
, the quotient and remainder are not defined. So “

 ” is undefined.
” is undefined.2.2Divisible, Divisor, Multiple


 is
is  , we say that
, we say that  divides
divides  . For example, “
. For example, “

 ” has remainder
” has remainder  , so
, so  divides
divides  . “
. “


 ” also has remainder
” also has remainder  , so
, so  divides
divides 
 .
. divides
divides  , then
, then  is a divisor of
is a divisor of  , and
, and  is a multiple of
is a multiple of  . For example,
. For example,  is a divisor of
is a divisor of  , and
, and  is a multiple of
is a multiple of  .
.
 are all the numbers that divide
are all the numbers that divide 
 , so in order: “
, so in order: “





























 ”. The multiples of
”. The multiples of  are “
are “

















 ”, which are all even numbers.
”, which are all even numbers. and
and 
 divide all integers, so their multiples are all integers. All integers except
divide all integers, so their multiples are all integers. All integers except  divide
divide  , so the divisors of
, so the divisors of  are all integers except
are all integers except  .
.2.3Common Divisors and Common Multiples
 and
and  is a number
is a number  that divides both
that divides both  and
and  . For example,
. For example,  divides both
divides both  and
and  , so
, so  is a common divisor of
is a common divisor of  and
and  .
. and
and  is a number
is a number  that is divisible by both
that is divisible by both  and
and  . For example,
. For example, 
 is divisible by both
is divisible by both  and
and  , so
, so 
 is a common multiple of
is a common multiple of  and
and  .
.2.4Greatest Common Divisor and Least Common Multiple
 and
and  is the largest of their common divisors, written as “
is the largest of their common divisors, written as “






 ”. The least common multiple of
”. The least common multiple of  and
and  is the smallest of their positive common multiples, written as “
is the smallest of their positive common multiples, written as “






 ”.
”.“gcd” stands for “greatest common divisor”, and “lcm” stands for “least common multiple”.
 are “
are “

















 ”, and the divisors of
”, and the divisors of  are “
are “

















 ”. Their common divisors are “
”. Their common divisors are “







 ”, so “
”, so “








 ”.
”. are “
are “










 ”, and of
”, and of  are “
are “













 ”. Their common multiples are “
”. Their common multiples are “








 ”, so “
”, so “









 ”.
”. and
and  , the rule “
, the rule “



















 ” holds. For example, “
” holds. For example, “






 ” gives “
” gives “



 ”. So if you know one of gcd or lcm, you can easily calculate the other.
”. So if you know one of gcd or lcm, you can easily calculate the other.2.5Euclidean Algorithm
- Let
 be the larger and
be the larger and  the smaller of the two integers.
the smaller of the two integers. - Let
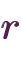 be the remainder of
be the remainder of 

 .
. - If
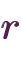

 , then
, then 














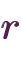
 . Repeat from step 1.
. Repeat from step 1. - If
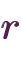

 , then
, then 








 . (Done)
. (Done)


 and
and 
 :
:



 ,
, 


 .
.




 gives remainder
gives remainder 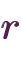


 , so
, so 




















 .
.






























 .
.



 gives remainder
gives remainder 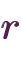

 , so
, so 











 .
.- Therefore,













 .
.
3.Prime Numbers


 is called a prime number if its only positive divisors are
is called a prime number if its only positive divisors are  and
and  . For example,
. For example,  is prime because its only positive divisors are
is prime because its only positive divisors are  and
and  .
.  is not prime because it also has
is not prime because it also has  as a divisor.
as a divisor.
 that cannot be divided by any positive integer other than
that cannot be divided by any positive integer other than  and itself. Numbers that are not prime are called composite numbers.
and itself. Numbers that are not prime are called composite numbers.

























 ”. There are infinitely many primes. Their pattern seems irregular, and people have studied it from ancient times to today.
”. There are infinitely many primes. Their pattern seems irregular, and people have studied it from ancient times to today.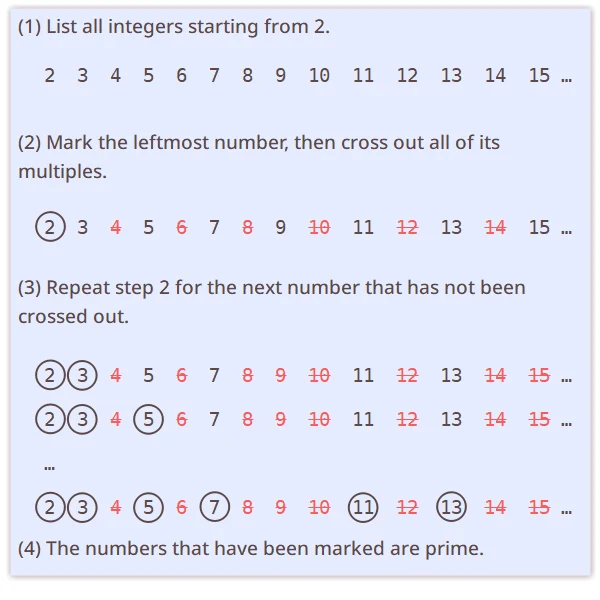
3.1Prime Factorization




 ”, “
”, “



 ”, “
”, “






 ”. This is called prime factorization.
”. This is called prime factorization.




 ”, so the prime factors of
”, so the prime factors of 
 are
are  and
and  .
.







 ” “
” “







 ” “
” “







 ” “
” “







 ” “
” “







 ” “
” “







 ”. This property is called the uniqueness of prime factorization, and it’s useful for proving other theorems.
”. This property is called the uniqueness of prime factorization, and it’s useful for proving other theorems. ” as a prime number because if we did, then: “
” as a prime number because if we did, then: “























 ” This would break the uniqueness of prime factorization.
” This would break the uniqueness of prime factorization.3.2Relatively Prime
 and
and  are relatively prime if they have no common divisors other than
are relatively prime if they have no common divisors other than  and
and 
 , that is, “
, that is, “








 ”. For example, “
”. For example, “









 ”, so
”, so  and
and 
 are relatively prime.
are relatively prime. and
and  , being relatively prime means they have no common prime factors. For example, “
, being relatively prime means they have no common prime factors. For example, “



 ” and “
” and “






 ” have no common prime factors, so they are relatively prime.
” have no common prime factors, so they are relatively prime.4.Congruence
 divided by
divided by  has remainder
has remainder  ”, and “
”, and “ divided by
divided by  also has remainder
also has remainder  ”. So in the world of remainders modulo
”. So in the world of remainders modulo  , “
, “

 ”. When two numbers have the same remainder when divided by
”. When two numbers have the same remainder when divided by  , we say they are congruent modulo
, we say they are congruent modulo  , and write “
, and write “







 ”.
”. and
and  have the same remainder when divided by
have the same remainder when divided by  , we write “
, we write “







 ”. If not, we write “
”. If not, we write “







 ”. These are called congruence equations.
”. These are called congruence equations.







 ” because both have remainder
” because both have remainder  . “
. “







 ” because their remainders are different.
” because their remainders are different.If 







 , then for any integer
, then for any integer  :
:








 ” implies “
” implies “











 ”.
”.5.Indeterminate Equation



 ” where you find values of variables that make the equation true. These values are called solutions.
” where you find values of variables that make the equation true. These values are called solutions.




 ” has solutions like “
” has solutions like “





 ” and “
” and “





 ”.
”.5.1Problem
Let “


 ” become “
” become “


 ” by reversing the digits. A 4-digit number
” by reversing the digits. A 4-digit number  becomes 4 times itself when reversed. Find the value of
becomes 4 times itself when reversed. Find the value of  .
.
5.2Solution
 be
be  ,
,  ,
,  ,
,  from left to right. For example, if
from left to right. For example, if 




 , then
, then 

 ,
, 

 ,
, 

 ,
, 

 . Then
. Then 
















 .
. gives
gives 














 , and since it’s 4 times the original, we get:
, and since it’s 4 times the original, we get:




































5.3Finding a


 ,
,  is not 4 digits, so
is not 4 digits, so 

 . If
. If 

 , then
, then 
 is 5 digits, so
is 5 digits, so 

 . So
. So  is either
is either  or
or  .
.

 , then the equation becomes “
, then the equation becomes “


































 ”. The rightmost digit is
”. The rightmost digit is  , but multiplying by
, but multiplying by  never gives a number ending in
never gives a number ending in  . So no solution. Therefore,
. So no solution. Therefore, 

 .
.5.4Finding d


 into the equation: “
into the equation: “


































 ”. The rightmost digit is
”. The rightmost digit is  , so
, so  must be a digit such that
must be a digit such that 



 ends in
ends in  . Only
. Only 




 and
and 




 work, so
work, so 

 or
or  .
.

 : equation becomes “
: equation becomes “

































 ”. Solving gives “
”. Solving gives “











 ”, which is negative for all
”, which is negative for all 

 to
to  . So
. So 

 , and
, and 

 .
.5.5Finding b and c


 : equation becomes “
: equation becomes “

































 ”. Solving gives “
”. Solving gives “









 ”. Only
”. Only 

 makes this an integer, so
makes this an integer, so 

 .
.


















 , so
, so 

 .
.

 ,
, 

 ,
, 

 ,
, 

 , and
, and 




 . Check:
. Check: 









 , which is the reverse of
, which is the reverse of 


 .
.