September 16, 2025
Kuina-chan
In Episode 1 of Kuina-chan Mathematics, I explain the rules and conventions of mathematics!
1.Axioms, Theorems, and Proofs
In mathematics, I generally start from a few assumptions that are considered true and logically derive other truths. These predetermined true assumptions are called axioms.
In addition to axioms, several rules are defined, and mathematics proceeds by using these axioms and rules to derive further truths.
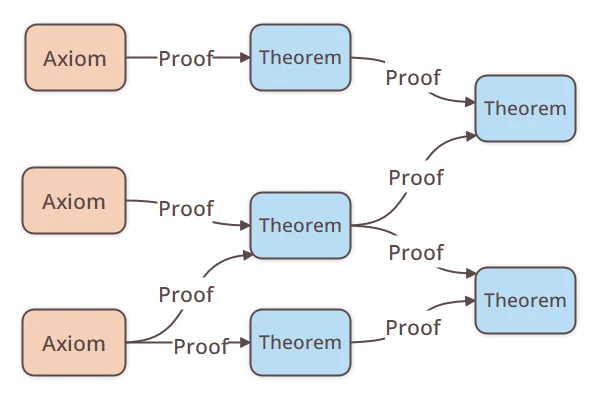
Newly derived truths, along with axioms, are called theorems, and the process of deriving a theorem is called a proof.
From another perspective, solving a math problem means using previously derived theorems to find a proof that shows the answer to the problem is itself a theorem.
2.Propositions and Logical Expressions
Now, statements like “
is true” or “
is true”—which can be judged as theorems or not—are called propositions.
is true” or “ is true”—which can be judged as theorems or not—are called propositions.There are several ways to handle propositions, but here I will use logical expressions with “true” and “false” to represent them. I define that “a proposition is a theorem if it is ‘true’, and not a theorem if it is ‘false’.” For example, if the proposition “ is true” is a theorem, then it is “true”. If “ is true” is not a theorem, then it is “false”.
is true” is a theorem, then it is “true”. If “ is true” is not a theorem, then it is “false”.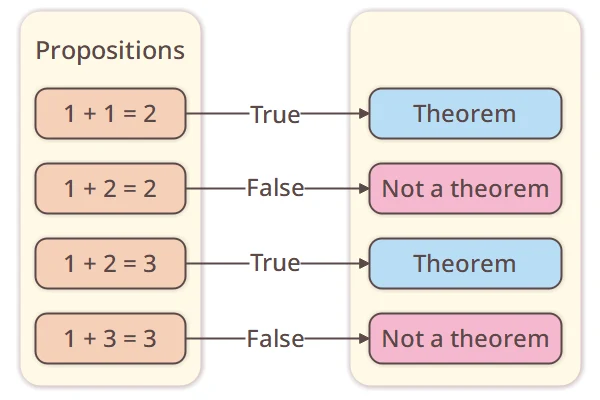
Note
Expressions that handle truth and falsehood like this are called “logical expressions.” In this article, I use logical expressions to represent whether a proposition is a theorem, but there are other ways to do this. For example, one approach is to consider a “tautology”—a proposition that is always true—as a theorem.
I will represent propositions using symbols like “
” and “
”. Then I consider combining them to create new propositions, such as “ implies ” or “ and ”.
” and “”. Then I consider combining them to create new propositions, such as “ implies ” or “ and ”.For example, if is the proposition “ is true” and is “ is true”, then “ or ” becomes the proposition “ is true, or is true”.
is the proposition “ is true” and is “ is true”, then “ or ” becomes the proposition “ is true, or is true”.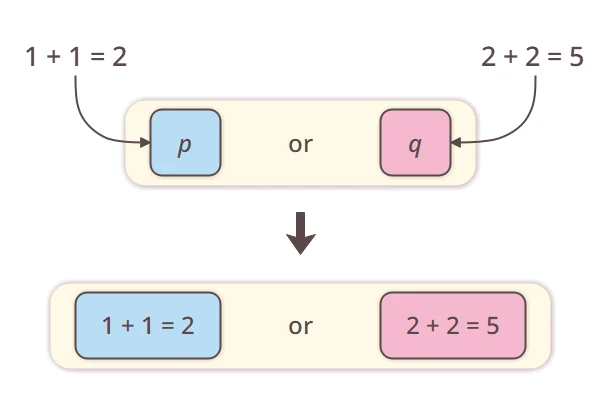
Usually, “or” is represented by the symbol “
” and “and” by “
”, so I write “” or “”. Thus, the proposition “ or ” can be written as “
”.
” and “and” by “”, so I write “” or “”. Thus, the proposition “ or ” can be written as “”.“ or ” means that if either or is true, then the whole is true. For example, if “ or is true, then at least one of ”“ or ”“ must be true. So the result of ”" is as follows:
or ” means that if either or is true, then the whole is true. For example, if “ or is true, then at least one of ”“ or ”“ must be true. So the result of ”" is as follows: |
|
|
|---|---|---|
| False | False | False |
| False | True | True |
| True | False | True |
| True | True | True |
On the other hand, “ and ” means that both and must be true for the whole to be true. So the result of “” is as follows:
and ” means that both and must be true for the whole to be true. So the result of “” is as follows: |
|
|
|---|---|---|
| False | False | False |
| False | True | False |
| True | False | False |
| True | True | True |
For example, if “” is true (a theorem) and “” is false (not a theorem), then “” is “true and false”, which is false and therefore not a theorem.
” is true (a theorem) and “” is false (not a theorem), then “” is “true and false”, which is false and therefore not a theorem.Note
Strictly speaking, I have decided that if a proposition created using logical “or” or “and” is true, then it is a theorem. From here on, I will continue to define that propositions which are true in logical expressions are theorems.
3.Properties of Logical Expressions
Next, I explain various properties of logical expressions that are necessary for proving theorems.
3.1Negation, Law of the Excluded Middle, and Contradiction
To express the negation of a proposition like “ is true”, I use the symbol “
”. For a proposition , “not ” is written as “”, and its result is as follows:
is true”, I use the symbol “”. For a proposition , “not ” is written as “”, and its result is as follows: |
|
|---|---|
| False | True |
| True | False |
From this table, I see that for any proposition , either “” or “” is true, meaning one of them is a theorem. This principle that there is no proposition for which both and are not theorems is called the Law of the Excluded Middle.
, either “” or “” is true, meaning one of them is a theorem. This principle that there is no proposition for which both and are not theorems is called the Law of the Excluded Middle.On the other hand, if both and are theorems, it is called a contradiction. This table also shows that contradictions do not occur.
and are theorems, it is called a contradiction. This table also shows that contradictions do not occur.By combining the Law of the Excluded Middle and contradiction, I can prove a negation by intentionally causing a contradiction, such as: “Assume is a theorem, which leads to a contradiction, therefore must be a theorem.”
is a theorem, which leads to a contradiction, therefore must be a theorem.”3.2Logical Implication
Another symbol in logical expressions is “ implies ”, written as “
”. This means “if holds, then holds”.
implies ”, written as “”. This means “if holds, then holds”.
If the proposition “” is a theorem, then whenever “ is true”, “ must also be true”.
” is a theorem, then whenever “ is true”, “ must also be true”.When “ is false”, “” can be anything. That is, if “ is false”, then regardless of “”, “” remains a theorem, so it is considered true.
is false”, “” can be anything. That is, if “ is false”, then regardless of “”, “” remains a theorem, so it is considered true.So when is false, is true regardless of . The result of “” is as follows:
is false, is true regardless of . The result of “” is as follows: |
|
|
|---|---|---|
| False | False | True |
| False | True | True |
| True | False | False |
| True | True | True |
For example, consider the theorem “If 
, then is odd.” If is not , the theorem says nothing about it, so whether is even or odd doesn’t affect the truth of the theorem. Thus, “False implies …” is always true.
, then is odd.” If is not , the theorem says nothing about it, so whether is even or odd doesn’t affect the truth of the theorem. Thus, “False implies …” is always true.3.3Equivalent Propositions
If the truth values of propositions and always match, they are said to be equivalent, written as “”.
and always match, they are said to be equivalent, written as “”.If being a theorem implies is a theorem, and vice versa, then and are equivalent. In logical expressions, this is written as “”. Therefore, “” can also be written using the symbol “
”.
being a theorem implies is a theorem, and vice versa, then and are equivalent. In logical expressions, this is written as “”. Therefore, “” can also be written using the symbol “”.If and are equivalent, proving one automatically proves the other. The result of “” is as follows:
and are equivalent, proving one automatically proves the other. The result of “” is as follows: |
|
|
|---|---|---|
| False | False | True |
| False | True | False |
| True | False | False |
| True | True | True |
3.4Converse, Inverse, and Contrapositive
Given a proposition of the form “”, the converse is “”, the inverse is “”, and the contrapositive is “”.
”, the converse is “”, the inverse is “”, and the contrapositive is “”.
Among these, the contrapositive is especially important because it is equivalent to the original proposition. For example, the proposition “If , then is odd” has the contrapositive “If is not odd, then 
”, and these two are equivalent.
, then is odd” has the contrapositive “If is not odd, then ”, and these two are equivalent.So when proving a proposition, I can prove its contrapositive instead.
3.5De Morgan’s Laws
Another important law is De Morgan’s Laws.
De Morgan’s Laws state that “” is equivalent to “”, and “” is equivalent to “”. In simpler terms, when removing the parentheses from “
”, the “” and “” inside switch places, and “” is distributed.
” is equivalent to “”, and “” is equivalent to “”. In simpler terms, when removing the parentheses from “”, the “” and “” inside switch places, and “” is distributed.For example, the proposition “It is not true that is even and 
” is equivalent to “ is not even or 
”. Similarly, “It is not true that is even or ” is equivalent to “ is not even and ”.
is even and ” is equivalent to “ is not even or ”. Similarly, “It is not true that is even or ” is equivalent to “ is not even and ”.These laws help simplify and reorganize complex propositions.
4.Predicate Functions
To handle more diverse theorems and propositions, I will delve deeper into logical expressions.
A predicate function is something that becomes a proposition when given a value. For example, “
is true” becomes the proposition “
is true” when and , so “ is true” is a predicate function.
is true” becomes the proposition “ is true” when and , so “ is true” is a predicate function.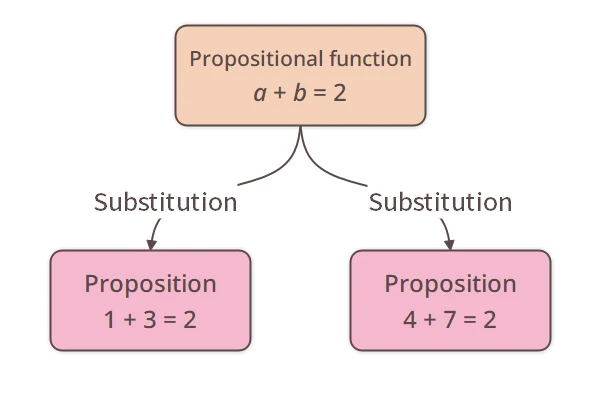
Predicate functions can take specific values like “” or “”, or they can take “all values” or “some value”. These are expressed by placing symbols “
” or “
” in front of variables like “
” or “
”, meaning “for all values” or “there exists a value” respectively.
” or “”, or they can take “all values” or “some value”. These are expressed by placing symbols “” or “” in front of variables like “” or “”, meaning “for all values” or “there exists a value” respectively.For example, if I take the predicate function “ is true” and substitute with , then write “ is true”, it means “for all values , is true”. Similarly, using “” and substituting with , I write “ is true”, which means “there exists a value such that is true”.
is true” and substitute with , then write “ is true”, it means “for all values , is true”. Similarly, using “” and substituting with , I write “ is true”, which means “there exists a value such that is true”.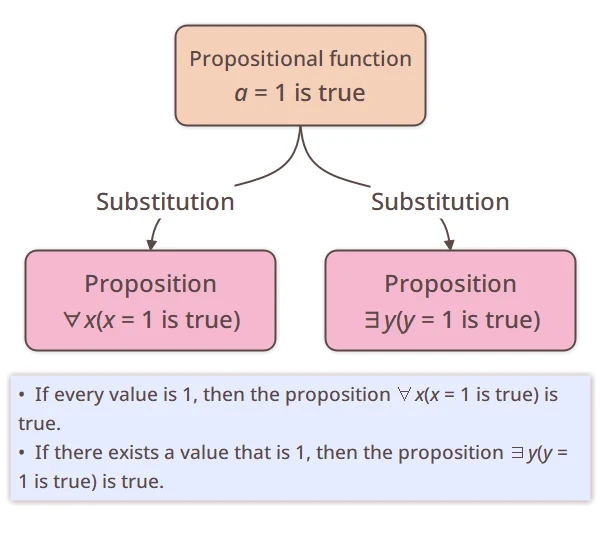
As a concrete example, suppose I have the predicate function “”. If I substitute and , the proposition “” is true. If I substitute and , the proposition “” is false.
”. If I substitute and , the proposition “” is true. If I substitute and , the proposition “” is false.Because “” exists, “” is not true for all and . Therefore, “” is false. However, since “” exists, there is at least one pair and for which “” is true. So “” is true.
” exists, “” is not true for all and . Therefore, “” is false. However, since “” exists, there is at least one pair and for which “” is true. So “” is true.5.Intuitionistic Logic
Finally, I will briefly introduce a different way of thinking called intuitionistic logic.
Until now, I assumed the Law of the Excluded Middle, which states that for any proposition , either or is a theorem. However, intuitionistic logic does not use the Law of the Excluded Middle. For example, in classical logic, I could say “I don’t know whether you like math, but you either like math or you don’t.” In intuitionistic logic, I can’t even say that—I say “I don’t know whether you like math or not, and I don’t know whether it’s one or the other.” This logic considers the possibility that I may not be able to prove something.
, either or is a theorem. However, intuitionistic logic does not use the Law of the Excluded Middle. For example, in classical logic, I could say “I don’t know whether you like math, but you either like math or you don’t.” In intuitionistic logic, I can’t even say that—I say “I don’t know whether you like math or not, and I don’t know whether it’s one or the other.” This logic considers the possibility that I may not be able to prove something.Because many theorems cannot be proven without assuming the Law of the Excluded Middle, intuitionistic logic is not mainstream in most areas of mathematics. However, it is often used in fields that study logic itself or in computer science, where it is highly compatible.
In this episode, I explained the basic rules of mathematics. Next time, let’s try proving a theorem from actual axioms!
