Episode 2 Sets and Natural Numbers - Kuina-chan Mathematics

September 16, 2025

Kuina-chan

In Episode 2 of Kuina-chan Mathematics, I explain the basics of mathematics and how proofs work through the example of “

”! This episode assumes you’ve read the series in order, beginning with Episode 1.

In Episode 1, I explained the fundamental rules of mathematics.

This time, I will prove “

” using specific axioms. But before that, let me explain the most basic concept in mathematics: sets. In mathematics, almost everything—including numbers like

—is considered to be made up of sets.

1.Naive Set Theory

1.1Sets and Elements

A set is a collection of things. The phrase “collection of things” is vague, but historically, sets began with this kind of intuitive idea. Eventually, they are defined rigorously.

Each “thing” in a set is called an element. If an element

belongs to a set $\bm{X}$ , we say that

is a member of $\bm{X}$ and write $\in$ $\bm{X}$ .

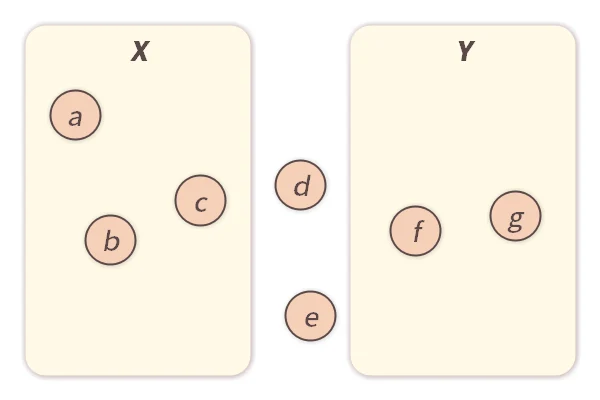
In this diagram, element

belongs to set $\bm{X}$ , so we write $\in$ $\bm{X}$ . On the other hand, elements

and

do not belong to $\bm{X}$ , so we write $\notin$ $\bm{X}$ and $\notin$ $\bm{X}$ .

1.2Extensional and Intensional Notation

There are two ways to describe which elements belong to a set: “extensional notation” and “intensional notation.”

Extensional notation lists the elements of a set. For example, if set $\bm{X}$ contains “dog,” “cat,” and “rabbit,” we write $\bm{X}$ $\{$ dogcatrabbit $\}$ .

Intensional notation describes the properties of the elements. For example, if set $\bm{X}$ contains all animals, we write $\bm{X}$ $\{$ is an animal $\}$ . You can use any symbol, like

, and write $\{$ symbolcondition using symbol $\}$ to mean “the set of all things that satisfy the condition.”

You can use either notation—whichever is simpler or clearer.

1.3Subsets and Equality

Next, let’s talk about relationships between sets. For example, if $\bm{X}$

$\{$ dog

cat

rabbit $\}$ and $\bm{Y}$

$\{$ dog

cat $\}$ , then all elements of $\bm{Y}$ are also in $\bm{X}$ . In this case, we say that $\bm{Y}$ is a subset of $\bm{X}$ and write $\bm{Y}$ $\subset$ $\bm{X}$ .

The symbols $\in$ (belongs to) and $\subset$ (is a subset of) look similar but have different meanings. $\in$ describes the relationship between an element and a set, while $\subset$ describes the relationship between two sets.

Note

In modern mathematics, almost everything is treated as a set, so even elements of sets are often sets themselves. This makes the distinction between “belongs to” and “is a subset of” a bit tricky. “Set X contains set Y as an element” means that Y is one of the elements of X. “Set X includes set Y as a subset” means that all elements of Y are also elements of X.

If all elements of sets $\bm{X}$ and $\bm{Y}$ are the same, then the sets are equal, and we write $\bm{X}$ $\bm{Y}$ . If they are not equal, we write $\bm{X}$ $\neq$ $\bm{Y}$ . The order of elements in a set doesn’t matter, and duplicates are treated as one. So if $\bm{X}$

$\{$ dog

cat

rabbit $\}$ and $\bm{Y}$

$\{$ rabbit

cat

dog

dog $\}$ , then $\bm{X}$ $\bm{Y}$ .

The symbols

and $\neq$ are also used to compare elements. If elements

and

are the same, we write

; if they are different, we write

$\neq$

1.4Sets of Sets

We can also think about sets whose elements are sets. For example, a set containing “dog” is written as $\{$ dog $\}$ , and a set containing that set is written as $\{$ $\{$ dog $\}$ $\}$ .

For example, if $\bm{X}$

$\{$ $\{$ dog $\}$

$\{$ cat $\}$ $\}$ , $\bm{Y}$

$\{$ $\{$ dog $\}$ $\}$ , and $\bm{Z}$

$\{$ dog $\}$ , then $\bm{Y}$ $\subset$ $\bm{X}$ and $\bm{Z}$ $\in$ $\bm{X}$ . Be careful whether you’re talking about elements and sets or sets and subsets.

1.5Union and Intersection

In Episode 1, I explained the logical operators “or ( $\lor$ )” and “and ( $\land$ ).” Sets have similar operations. In set theory, “or” is represented by $\cup$ and “and” by $\cap$ . For sets $\bm{X}$ and $\bm{Y}$ , we write $\bm{X}$ $\cup$ $\bm{Y}$ and $\bm{X}$ $\cap$ $\bm{Y}$ .

For example, suppose $\bm{X}$

$\{$ honey

sugar

grapefruit $\}$ is the set of sweet things, and $\bm{Y}$

$\{$ vinegar

lemon

grapefruit $\}$ is the set of sour things. Then, “sweet or sour” is $\bm{X}$ $\cup$ $\bm{Y}$

$\{$ honey

sugar

grapefruit

vinegar

lemon $\}$ , and “sweet and sour” is $\bm{X}$ $\cap$ $\bm{Y}$

$\{$ grapefruit $\}$ .

So $\cup$ combines sets, and $\cap$ extracts their common elements.

1.6Empty Set

A set with no elements is called the empty set, written as $\emptyset$ . For example, if set $\bm{X}$ has no elements, we write $\bm{X}$

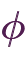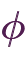$\emptyset$ . This symbol looks like the Greek letter $\phi$ (phi), but it’s a different symbol.

Note that $\emptyset$ and $\{$ $\emptyset$ $\}$ are different sets. $\emptyset$ has no elements, while $\{$ $\emptyset$ $\}$ is a set whose only element is the empty set.

2.Natural Numbers

Now, let’s define “natural numbers” using sets so we can prove “

”.

Natural numbers are the sequence

$\dots$ . Whether

is included depends on the context. In modern mathematics, it’s usually included, but in number theory, it’s often excluded. Here, I will include it.

Let’s define the set of all natural numbers $\mathbb{N}$ . You might think it’s enough to write $\mathbb{N}$

$\{$

$\dots$ $\}$ , but this assumes we already know the sequence continues with

$\dots$ . That’s not rigorous. So instead, I will use the Peano axioms to define natural numbers. According to the Peano axioms, natural numbers satisfy the following structure:

In simpler terms, we start from

, then define

as the next number,

as the next after that, and so on—forming a straight path with no branches or loops. Here’s a diagram showing the structure defined by the Peano axioms: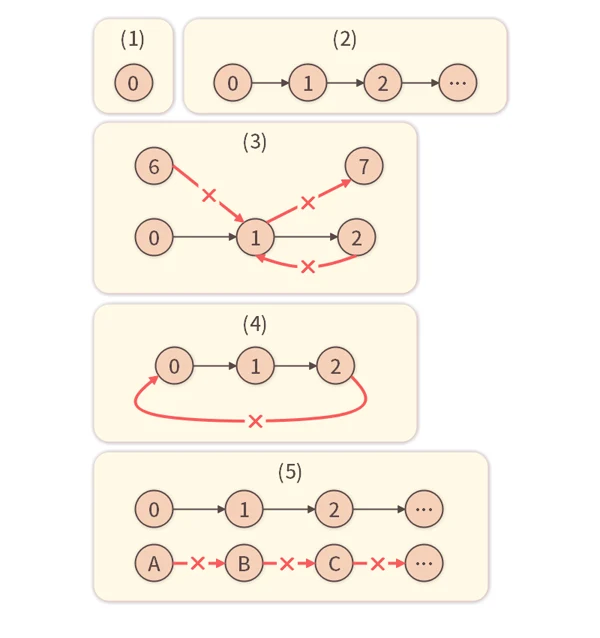

Conditions (3) and (4) eliminate branches and loops, and (5) excludes any sequences other than

$\dots$ . This ensures that natural numbers form a single straight path.

The key idea is that natural numbers don’t exist as specific objects. Instead, anything that satisfies this structure is called a natural number. This allows us to treat many things as natural numbers.

Now, let’s construct natural numbers using only sets. Since sets are the basic building blocks of mathematics, if we can build natural numbers from sets, we can treat them as mathematical objects.

For example, if we represent

as the empty set $\emptyset$ and define the successor of

as $\{$ $\}$ then $\emptyset$

; $\{$ $\emptyset$ $\}$

; $\{$ $\{$ $\emptyset$ $\}$ $\}$

; $\{$ $\{$ $\{$ $\emptyset$ $\}$ $\}$ $\}$

; and $\{$ $\{$ $\{$ $\{$ $\emptyset$ $\}$ $\}$ $\}$ $\}$

. This satisfies the Peano axioms, so these are natural numbers.

Another method: define

as $\emptyset$ and the successor of

as $\cup$ $\{$ $\}$ , then $\emptyset$

; $\emptyset$ $\cup$ $\{$ $\emptyset$ $\}$

$\{$ $\emptyset$ $\}$

$\{$

$\}$

; $\{$ $\emptyset$ $\}$ $\cup$ $\{$ $\{$ $\emptyset$ $\}$ $\}$

$\{$ $\emptyset$

$\{$ $\emptyset$ $\}$ $\}$

$\{$

$\}$

; and so on. This also satisfies the Peano axioms, so it’s valid.

There are many ways to construct natural numbers from sets. The specific method doesn’t matter—as long as it satisfies the Peano axioms. From now on, I will represent these natural numbers as the set $\mathbb{N}$ $\{$ $\dots$ $\}$ .

3.Axiomatic Set Theory

3.1Russell’s Paradox

So far, I’ve explained sets intuitively. But it’s known that this intuitive approach can lead to logical contradictions. One famous example is Russell’s Paradox.

First, imagine a set called “Words” that contains all words. Since “Words” is itself a word, it belongs to the set. So we have: Words

$\{$ dog

apple

Words

$\dots$ $\}$ .

Next, imagine a set called “Emojis” that contains all emojis. “Emojis” itself is not an emoji, so it does not belong to the set: Emojis

$\{$

$\dots$ $\}$ .

This shows that sets can be of two types: those that contain themselves (like “Words”) and those that do not contain themselves (like “Emojis”).

Now, consider the set of all sets that do not contain themselves. Since “Emojis” does not contain itself, it belongs to this set: Non-self-membered sets $\{$ Emojis $\dots$ $\}$ . But does this set contain itself? In other words, do we end up with Non-self-membered sets $\{$ EmojisNon-self-membered sets $\dots$ $\}$ ?

If it does, then it shouldn’t—because it only contains sets that do not contain themselves. If it doesn’t, then it should—because it qualifies as a set that does not contain itself.

This contradiction means the question is not a valid proposition. As I explained in Episode 1, a proposition must be either true or false. So allowing sets like “the set of all sets that do not contain themselves” leads to logical inconsistency.

3.2Axiomatic Set Theory

To avoid this, mathematicians moved away from intuitive definitions like “a collection of things” and instead defined sets using axioms that rigorously specify what counts as a set. This approach is called axiomatic set theory. The intuitive version is called naive set theory.