January 17, 2026
Kuina-chan
In Episode 4 of Kuina-chan Mathematics, I explain functions and mappings that connect numbers to other numbers! This episode assumes you’ve read the series in order, beginning with Episode 1.
In Episode 3, I defined the set of integers 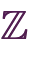 . This time, I explain rational numbers
. This time, I explain rational numbers  , real numbers
, real numbers  , and the concepts of functions and mappings.
, and the concepts of functions and mappings.
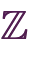 . This time, I explain rational numbers
. This time, I explain rational numbers  , real numbers
, real numbers  , and the concepts of functions and mappings.
, and the concepts of functions and mappings.1.Rational and Real Numbers
So far, we’ve dealt with integers, but now let’s explore more detailed numbers: rational numbers and real numbers. These are what we usually call “decimals.”
1.1Rational Numbers
A rational number is a number that can be expressed as a fraction of integer over integer, where the denominator is not zero. For example, 

 ,
, 

 , and
, and 


 are rational numbers. Even a decimal like
are rational numbers. Even a decimal like 





 is rational because it can be written as the fraction
is rational because it can be written as the fraction 


 .
.


 ,
, 

 , and
, and 


 are rational numbers. Even a decimal like
are rational numbers. Even a decimal like 





 is rational because it can be written as the fraction
is rational because it can be written as the fraction 


 .
.We’ll denote the set of all rational numbers as  . That is,
. That is, 
























 .
.
 . That is,
. That is, 
























 .
.1.2Converting Decimals to Fractions
By the way, repeating decimals like 












 can always be converted into a fraction of integer over integer, making them rational numbers. Even
can always be converted into a fraction of integer over integer, making them rational numbers. Even 

 is a repeating decimal (
is a repeating decimal (





 ), so it’s rational.
), so it’s rational.













 can always be converted into a fraction of integer over integer, making them rational numbers. Even
can always be converted into a fraction of integer over integer, making them rational numbers. Even 

 is a repeating decimal (
is a repeating decimal (





 ), so it’s rational.
), so it’s rational.Here’s how to convert a repeating decimal like 












 into a fraction:
into a fraction:













 into a fraction:
into a fraction:- Let















 .
. - Multiply both sides by a power of 10 so that one full cycle of the repeating digits appears to the left of the decimal point. That is,






















 .
. - Subtract the original equation















 from both sides:
from both sides: 







 .
. - Rearranging gives

















 , so
, so 




















 .
.
Any repeating decimal can be converted into a fraction using this method.
1.3Irrational Numbers
On the other hand, non-repeating decimals are called irrational numbers. Irrational numbers cannot be expressed as a fraction of integer over integer. Examples include the number 








 (pi) and the number whose square is 2,
(pi) and the number whose square is 2, 









 .
.









 (pi) and the number whose square is 2,
(pi) and the number whose square is 2, 









 .
.Combining rational and irrational numbers gives us real numbers. We’ll denote the set of all real numbers as  .
.
 .
.Note
In this definition of real numbers, I used the vague idea of “decimals,” but there are more rigorous ways to define them. One such method is to consider that when you line up rational numbers densely, they can get arbitrarily close to some number. That number might not be rational, and we define such numbers as irrational. Rational and irrational numbers together form the real numbers.
All natural numbers are included in the integers. All integers are included in the rational numbers. Therefore, the inclusion relationships among the types of numbers we’ve introduced so far are as follows:
Natural numbers 
 Integers
Integers 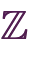
 Rational numbers
Rational numbers 
 Real numbers
Real numbers 
1.4Basic Operations
Rational and real numbers support the same operations as integers. For any two numbers  and
and  , we can define addition
, we can define addition 

 , subtraction
, subtraction 

 , multiplication
, multiplication 

 , exponentiation
, exponentiation 
 , and absolute value
, and absolute value 

 . Also, for
. Also, for 

 , division
, division 

 is defined. However, if
is defined. However, if 

 , such as
, such as 

 , the expression is undefined.
, the expression is undefined.
 and
and  , we can define addition
, we can define addition 

 , subtraction
, subtraction 

 , multiplication
, multiplication 

 , exponentiation
, exponentiation 
 , and absolute value
, and absolute value 

 . Also, for
. Also, for 

 , division
, division 

 is defined. However, if
is defined. However, if 

 , such as
, such as 

 , the expression is undefined.
, the expression is undefined.Additionally, real numbers allow us to define square roots. The square root of  is a number
is a number  such that
such that 


 . For example, the square roots of
. For example, the square roots of  are
are  and
and 
 , since
, since 


 and
and 





 . Similarly, the square roots of
. Similarly, the square roots of  are
are  and
and 
 .
.
 is a number
is a number  such that
such that 


 . For example, the square roots of
. For example, the square roots of  are
are  and
and 
 , since
, since 


 and
and 





 . Similarly, the square roots of
. Similarly, the square roots of  are
are  and
and 
 .
.The positive square root is called the principal square root and is denoted by  . So
. So 

 and
and 

 .
.
 . So
. So 

 and
and 

 .
.We can extend this idea: a number  that satisfies
that satisfies 


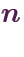 is called the
is called the  th root of
th root of  . The positive
. The positive  th root of
th root of  is denoted by
is denoted by ![\sqrt[n]{x}](/m/sqrt_n_x.webp) . For example, since
. For example, since 



 , we have
, we have ![\sqrt[4]{16}](/m/sqrt_4_16.webp)

 .
.
 that satisfies
that satisfies 


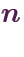 is called the
is called the  th root of
th root of  . The positive
. The positive  th root of
th root of  is denoted by
is denoted by ![\sqrt[n]{x}](/m/sqrt_n_x.webp) . For example, since
. For example, since 



 , we have
, we have ![\sqrt[4]{16}](/m/sqrt_4_16.webp)

 .
.Here are some values of principal square roots:
| Principal Square Root |
|---|
   |
   |
               |
               |
   |
               |
               |
               |
               |
   |
If we graph the principal square root 

 , it looks like the image below. When
, it looks like the image below. When  is less than 0, there is no real number whose square is
is less than 0, there is no real number whose square is  , so
, so  is undefined.
is undefined.


 , it looks like the image below. When
, it looks like the image below. When  is less than 0, there is no real number whose square is
is less than 0, there is no real number whose square is  , so
, so  is undefined.
is undefined.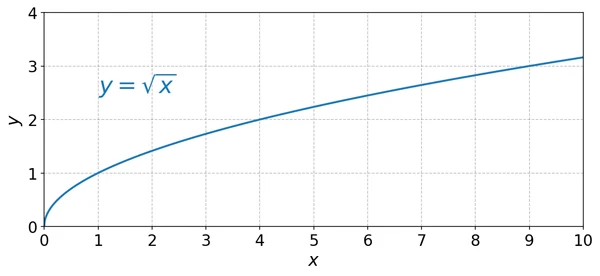
By the way,  is an irrational number. Let’s prove it since it’s simple.
is an irrational number. Let’s prove it since it’s simple.
 is an irrational number. Let’s prove it since it’s simple.
is an irrational number. Let’s prove it since it’s simple.- We’ll use proof by contradiction: assume
 is rational and show that this leads to a contradiction.
is rational and show that this leads to a contradiction. - Suppose
 is rational. Since
is rational. Since 

 , we can express it as
, we can express it as 



 for some positive integers
for some positive integers  and
and  .
. - Squaring both sides gives






 . Multiply both sides by
. Multiply both sides by 
 to get
to get 




 .
. - Since
 and
and  are positive integers, both sides are positive integers and can be prime factorized. By the uniqueness of prime factorization, both sides must have the same prime factors.
are positive integers, both sides are positive integers and can be prime factorized. By the uniqueness of prime factorization, both sides must have the same prime factors. - Squaring
 and
and  doubles the number of each prime factor. So the number of 2s in the prime factorization of
doubles the number of each prime factor. So the number of 2s in the prime factorization of 
 and
and 
 is even. But in
is even. But in 




 , the number of 2s is odd. This is a contradiction.
, the number of 2s is odd. This is a contradiction. - Therefore, the assumption that “
 is rational” is false, and by the law of the excluded middle, the statement “
is rational” is false, and by the law of the excluded middle, the statement “ is not rational” is true. That is,
is not rational” is true. That is,  is irrational. (End of proof)
is irrational. (End of proof)
This method of assuming 
 and deriving a contradiction to prove
and deriving a contradiction to prove  is called proof by contradiction.
is called proof by contradiction.

 and deriving a contradiction to prove
and deriving a contradiction to prove  is called proof by contradiction.
is called proof by contradiction.2.Polynomial Equations
2.1Linear Equations
Now let’s try solving equations with real numbers. Here’s a simple problem:
Problem
Find all  that satisfy
that satisfy 




 .
.
An equation of the form 




 (where
(where 

 ) is called a linear equation. You can solve linear equations easily by adding or multiplying both sides by the same number.
) is called a linear equation. You can solve linear equations easily by adding or multiplying both sides by the same number.





 (where
(where 

 ) is called a linear equation. You can solve linear equations easily by adding or multiplying both sides by the same number.
) is called a linear equation. You can solve linear equations easily by adding or multiplying both sides by the same number.- Add 3 to both sides of





 to get
to get 


 .
. - Divide both sides of



 by
by  to get
to get 

 .
. - Therefore, the solution to





 is
is 

 .
.
2.2Quadratic Equations
Next, let’s try a slightly more complex problem:
Problem
Find all  that satisfy
that satisfy 








 .
.
An equation of the form 








 (where
(where 

 ) is called a quadratic equation. If you can transform it into the form
) is called a quadratic equation. If you can transform it into the form 










 , it’s easy to solve. So let’s aim for that form.
, it’s easy to solve. So let’s aim for that form.









 (where
(where 

 ) is called a quadratic equation. If you can transform it into the form
) is called a quadratic equation. If you can transform it into the form 










 , it’s easy to solve. So let’s aim for that form.
, it’s easy to solve. So let’s aim for that form.First, expand the left-hand side of 










 . Using the rule
. Using the rule 



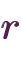






 , we apply it repeatedly to remove the parentheses:
, we apply it repeatedly to remove the parentheses: 















































 .
.











 . Using the rule
. Using the rule 



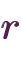






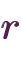 , we apply it repeatedly to remove the parentheses:
, we apply it repeatedly to remove the parentheses: 















































 .
.Now compare this with the problem equation 








 . We want
. We want 



 and
and 




 . Trying some values, we find
. Trying some values, we find 

 and
and 


 work. Substituting gives:
work. Substituting gives: 


















 .
.









 . We want
. We want 



 and
and 




 . Trying some values, we find
. Trying some values, we find 

 and
and 


 work. Substituting gives:
work. Substituting gives: 


















 .
.So the original equation 








 can be transformed into
can be transformed into 













 . This means we need to find
. This means we need to find  such that
such that 










 . That is, at least one of the factors must be zero.
. That is, at least one of the factors must be zero.









 can be transformed into
can be transformed into 













 . This means we need to find
. This means we need to find  such that
such that 










 . That is, at least one of the factors must be zero.
. That is, at least one of the factors must be zero.If 



 , then
, then 


 . If
. If 



 , then
, then 

 . Both can’t be zero at the same time. So these are all the solutions. Therefore, the solutions to
. Both can’t be zero at the same time. So these are all the solutions. Therefore, the solutions to 








 are
are 




 .
.




 , then
, then 


 . If
. If 



 , then
, then 

 . Both can’t be zero at the same time. So these are all the solutions. Therefore, the solutions to
. Both can’t be zero at the same time. So these are all the solutions. Therefore, the solutions to 








 are
are 




 .
.2.3Quadratic Formula
By the way, you can also solve quadratic equations using the quadratic formula shown below:

Indeed, this gives the same solutions as before.
3.Mappings
Finally, let me explain functions and mappings.
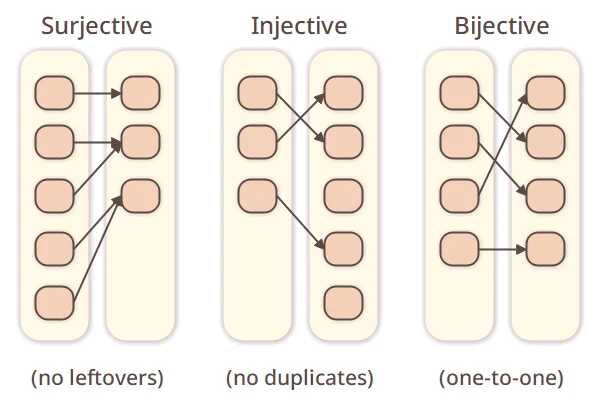
A mapping is a way to assign each element of one set to an element of another set. It’s also called a function. In the diagram below, the arrows connecting elements represent a mapping.
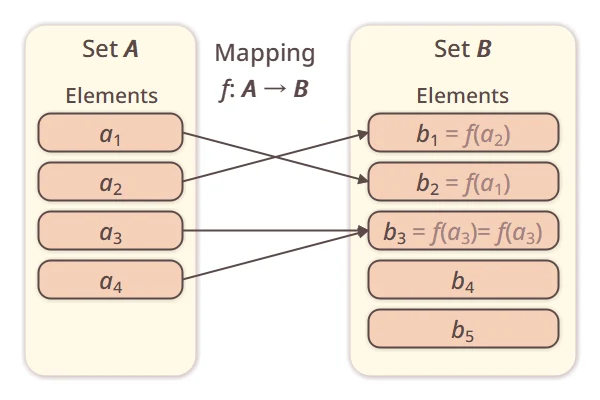
If a mapping  assigns elements of set
assigns elements of set  to elements of set
to elements of set  , we write it as
, we write it as 



 . The element of
. The element of  that corresponds to an element
that corresponds to an element  of
of  is written as
is written as 


 . For example, in the diagram, element
. For example, in the diagram, element 
 corresponds to
corresponds to 
 , so
, so 






 .
.
 assigns elements of set
assigns elements of set  to elements of set
to elements of set  , we write it as
, we write it as 



 . The element of
. The element of  that corresponds to an element
that corresponds to an element  of
of  is written as
is written as 


 . For example, in the diagram, element
. For example, in the diagram, element 
 corresponds to
corresponds to 
 , so
, so 






 .
.In 



 , for every element
, for every element  in
in  , there is exactly one corresponding element
, there is exactly one corresponding element 


 in
in  . There are no missing or multiple correspondences.
. There are no missing or multiple correspondences.




 , for every element
, for every element  in
in  , there is exactly one corresponding element
, there is exactly one corresponding element 


 in
in  . There are no missing or multiple correspondences.
. There are no missing or multiple correspondences.Mappings can also be defined between the same set. That is, 



 is allowed.
is allowed.




 is allowed.
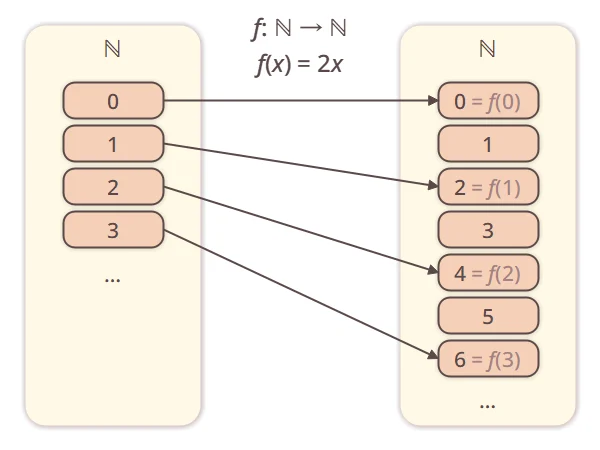
is allowed.For example, consider the mapping 





 on the set of natural numbers
on the set of natural numbers  . This is a mapping
. This is a mapping 



 .
.






 on the set of natural numbers
on the set of natural numbers  . This is a mapping
. This is a mapping 



 .
.
3.1Surjective, Injective, Bijective
In 



 , if the elements of
, if the elements of  cover all elements of
cover all elements of  without omission, then
without omission, then  is called surjective. More precisely, if the set of all
is called surjective. More precisely, if the set of all 


 for
for  in
in  equals
equals  , then
, then  is surjective.
is surjective.




 , if the elements of
, if the elements of  cover all elements of
cover all elements of  without omission, then
without omission, then  is called surjective. More precisely, if the set of all
is called surjective. More precisely, if the set of all 


 for
for  in
in  equals
equals  , then
, then  is surjective.
is surjective.If each element of  maps to a unique element in
maps to a unique element in  without duplication, then
without duplication, then  is called injective. More precisely, for any two distinct elements
is called injective. More precisely, for any two distinct elements  and
and  in
in  , if
, if 







 , then
, then  is injective.
is injective.
 maps to a unique element in
maps to a unique element in  without duplication, then
without duplication, then  is called injective. More precisely, for any two distinct elements
is called injective. More precisely, for any two distinct elements  and
and  in
in  , if
, if 







 , then
, then  is injective.
is injective.If a mapping  is both surjective and injective, then it’s called bijective. In this case, the elements of
is both surjective and injective, then it’s called bijective. In this case, the elements of  and
and  correspond one-to-one.
correspond one-to-one.
 is both surjective and injective, then it’s called bijective. In this case, the elements of
is both surjective and injective, then it’s called bijective. In this case, the elements of  and
and  correspond one-to-one.
correspond one-to-one.Here’s a diagram showing the concepts of surjective, injective, and bijective mappings:
3.2Inverse Mapping
The inverse mapping of a mapping  is a mapping that reverses the direction of correspondence. It’s denoted as
is a mapping that reverses the direction of correspondence. It’s denoted as 

 . To explain it precisely: if we have mappings
. To explain it precisely: if we have mappings 



 and
and 



 , and for every
, and for every  in
in  ,
, 







 , and for every
, and for every  in
in  ,
, 







 , then
, then  is the inverse mapping of
is the inverse mapping of  , written as
, written as 



 .
.
 is a mapping that reverses the direction of correspondence. It’s denoted as
is a mapping that reverses the direction of correspondence. It’s denoted as 

 . To explain it precisely: if we have mappings
. To explain it precisely: if we have mappings 



 and
and 



 , and for every
, and for every  in
in  ,
, 







 , and for every
, and for every  in
in  ,
, 







 , then
, then  is the inverse mapping of
is the inverse mapping of  , written as
, written as 



 .
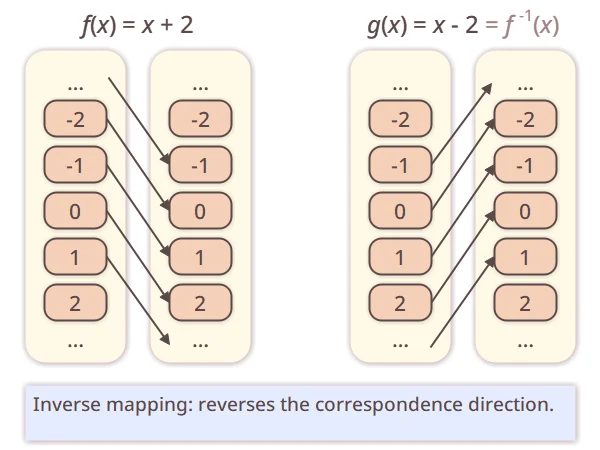
.For example, consider the mapping 






 on integers
on integers 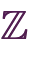 , and the mapping
, and the mapping 






 on
on 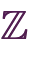 . Since the direction of correspondence is reversed,
. Since the direction of correspondence is reversed,  is the inverse mapping of
is the inverse mapping of  , i.e.,
, i.e., 



 .
.







 on integers
on integers 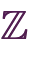 , and the mapping
, and the mapping 






 on
on 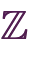 . Since the direction of correspondence is reversed,
. Since the direction of correspondence is reversed,  is the inverse mapping of
is the inverse mapping of  , i.e.,
, i.e., 



 .
.
By the way, if a mapping  is not bijective, then it has no inverse mapping. If
is not bijective, then it has no inverse mapping. If  is bijective, then it always has a unique inverse mapping
is bijective, then it always has a unique inverse mapping 

 .
.
 is not bijective, then it has no inverse mapping. If
is not bijective, then it has no inverse mapping. If  is bijective, then it always has a unique inverse mapping
is bijective, then it always has a unique inverse mapping 

 .
.In this article, I explained real numbers and mappings. Next time, I’ll explain various geometric shapes like triangles and circles!


